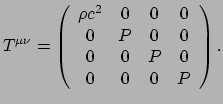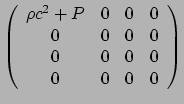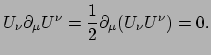Next: Wiskunde II - Curvelineaire
Up: De speciale relativiteitstheorie
Previous: De extra traagheid van
Contents
Vergelijking (223) geeft de energie die nodig is om een gas te
versnellen. De energie is echter afhankelijk van het referentiestelsel, want
het is de 0-component van de vierimpuls gegeven
door vergelijking (216). Alhoewel deze vierimpuls een
volledige beschrijving geeft van de energie en impuls van een individueel
deeltje, zullen we in het vervolg vaak uitgebreide systemen bespreken die
zijn samengesteld uit grote aantallen deeltjes. In plaats van het toekennen
van vierimpulsen aan ieder individueel deeltje, kiezen we ervoor om het
hele systeem als een vloeistof te beschrijven - een continuum dat gekarakteriseerd
wordt door macroscopische grootheden als druk, dichtheid, entropie en viscositeit.
In het algemeen heeft deze vloeistof een bepaalde viersnelheidveld.
Een enkele impuls viervectorveld is onvoldoende om de energie en impuls
van de vloeistof te beschrijven. We definiëren een energie-impuls tensor
(ook wel de stress tensor genoemd) met componenten
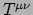 . Deze
symmetrische
. Deze
symmetrische
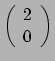 tensor
vertelt ons alles wat we moeten weten van de energie-achtige eigenschappen
van een systeem: energiedichtheid, druk, spanning, etc. Een algemene definitie
van
tensor
vertelt ons alles wat we moeten weten van de energie-achtige eigenschappen
van een systeem: energiedichtheid, druk, spanning, etc. Een algemene definitie
van
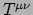 is de flux van vierimpuls
is de flux van vierimpuls 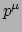 door een oppervlak met
constante
door een oppervlak met
constante 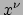 . Beschouw bijvoorbeeld een oneindig klein vloeistofelement
in zijn rustsysteem. Dan is
. Beschouw bijvoorbeeld een oneindig klein vloeistofelement
in zijn rustsysteem. Dan is 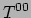 de flux van
de flux van 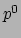 (energie) in de
(energie) in de
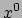 (tijd) richting: het is de energiedichtheid
(tijd) richting: het is de energiedichtheid 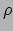 in het rustsysteem.
Op dezelfde manier zien we dat in dit frame
in het rustsysteem.
Op dezelfde manier zien we dat in dit frame
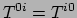 de impulsdichtheid
is. De ruimtelijke componenten
de impulsdichtheid
is. De ruimtelijke componenten 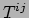 zijn de impulsflux, ofwel de
stress, en vertegenwoordigen de krachten tussen aangrenzende volume elementen.
Een diagonale term als
zijn de impulsflux, ofwel de
stress, en vertegenwoordigen de krachten tussen aangrenzende volume elementen.
Een diagonale term als 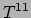 geeft de
geeft de 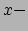 component van de kracht die
per eenheid oppervlakte door het element wordt uitgeoefend in de
component van de kracht die
per eenheid oppervlakte door het element wordt uitgeoefend in de
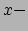 richting. We interpreteren dit als de
richting. We interpreteren dit als de 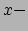 component van de druk (
component van de druk (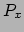 ).
De druk heeft drie dergelijke componenten,
).
De druk heeft drie dergelijke componenten,
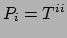 , in het
rustsysteem van de vloeistof.
, in het
rustsysteem van de vloeistof.
We zullen het bovenstaande concreter maken door `stof' (engels: dust) als
voorbeeld te nemen. Kosmologen hebben de neiging om materie als synoniem
voor stof te gebruiken. We definiëren stof in de vlakke ruimtetijd
als een verzameling deeltjes die in rust zijn ten opzichte van elkaar.
Het viervector snelheidsveld 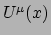 is de constante viersnelheid
van de individuele deeltjes. De componenten zijn hetzelfde op elk
punt. We definiëren de flux viervector als
is de constante viersnelheid
van de individuele deeltjes. De componenten zijn hetzelfde op elk
punt. We definiëren de flux viervector als
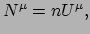 |
(218) |
met 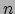 de deeltjesdichtheid gemeten in het rustsysteem. Dan is
de deeltjesdichtheid gemeten in het rustsysteem. Dan is 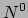 de deeltjesdichtheid gemeten in een ander systeem, terwijl
de deeltjesdichtheid gemeten in een ander systeem, terwijl 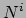 de
deeltjesflux is in de
de
deeltjesflux is in de 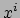 -richting. Verder nemen we aan dat elk deeltje
massa
-richting. Verder nemen we aan dat elk deeltje
massa 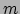 heeft. In het rustsysteem wordt de energiedichtheid van de
stof gegeven door
heeft. In het rustsysteem wordt de energiedichtheid van de
stof gegeven door
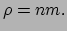 |
(219) |
Per definitie specificeert de energiedichtheid de stof volledig.
Echter 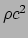 meet de energiedichtheid in het rustsysteem. Hoe
zit het met de andere systemen? Merk op dat zowel
meet de energiedichtheid in het rustsysteem. Hoe
zit het met de andere systemen? Merk op dat zowel 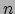 als
als 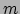 de
de 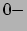 componenten zijn van viervectoren in hun rustsysteem,
namelijk
componenten zijn van viervectoren in hun rustsysteem,
namelijk
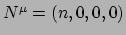 en
en
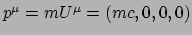 . We zien dus
dat
. We zien dus
dat 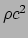 de
de
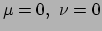 component is van de tensor
component is van de tensor
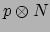 gemeten in het rustsysteem. Dit leidt tot de
volgende definitie van de energie-impuls tensor voor stof,
gemeten in het rustsysteem. Dit leidt tot de
volgende definitie van de energie-impuls tensor voor stof,
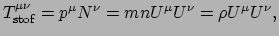 |
(220) |
met 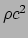 de energiedichtheid in het rustsysteem. We zien dat
de druk van het stof in elke richting gelijk is aan nul. Dat klopt
ook wel, omdat wij stof gedefinieerd hebben als een verzameling
deeltjes zonder random bewegingen.
de energiedichtheid in het rustsysteem. We zien dat
de druk van het stof in elke richting gelijk is aan nul. Dat klopt
ook wel, omdat wij stof gedefinieerd hebben als een verzameling
deeltjes zonder random bewegingen.
Stof in onvoldoende voor een algemene beschrijving van belangrijke
fenomenen in de ART. Hiervoor is het concept van een `perfecte vloeistof'
nodig. Een perfecte vloeistof kan volledig worden gespecificeerd
door twee grootheden: de energiedichtheid 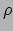 in het rustsysteem,
en een isotrope druk
in het rustsysteem,
en een isotrope druk 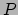 in het rustsysteem. De parameter
in het rustsysteem. De parameter 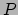 geeft
de druk in elke richting. Een consequentie van de isotropie is dat
geeft
de druk in elke richting. Een consequentie van de isotropie is dat
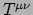 diagonaal is in het rustsysteem. Verder moeten de
diagonale componenten allemaal gelijk zijn:
diagonaal is in het rustsysteem. Verder moeten de
diagonale componenten allemaal gelijk zijn:
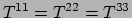 .
Er zijn dus slechts twee onafhankelijke parameters en dat is de
energiedichtheid
.
Er zijn dus slechts twee onafhankelijke parameters en dat is de
energiedichtheid
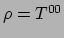 en de druk
en de druk
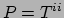 . De
energie-impuls tensor van een perfecte vloeistof heeft daarmee
de volgende vorm in het rustsysteem,
. De
energie-impuls tensor van een perfecte vloeistof heeft daarmee
de volgende vorm in het rustsysteem,
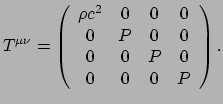 |
(221) |
We willen uiteraard een formule die geldig is in elk systeem,
een tensorvergelijking. Voor stof hadden we
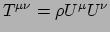 ,
dus we gokken op
,
dus we gokken op
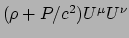 . Dit geeft
. Dit geeft
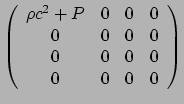 |
(222) |
en we zien dat niet correct is. We dienen er de volgende bijdrage
bij op te tellen,
 |
(223) |
hetgeen we kunnen schrijven als
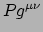 , met
, met
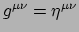 in de SRT. Hiermee vinden we voor de algemene vorm van de energie-impuls tensor
voor een perfecte vloeistof
in de SRT. Hiermee vinden we voor de algemene vorm van de energie-impuls tensor
voor een perfecte vloeistof
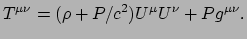 |
(224) |
Gegeven dat vergelijking (227) de vorm van
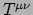 in
het rustsysteem is, en dat vergelijking (230) een tensorvergelijking
is die in het rustsysteem reduceert tot vergelijking (227), weten
we dat we met vergelijking (230) de correcte uitdrukking voor
elk coördinatenstelsel hebben gevonden.
in
het rustsysteem is, en dat vergelijking (230) een tensorvergelijking
is die in het rustsysteem reduceert tot vergelijking (227), weten
we dat we met vergelijking (230) de correcte uitdrukking voor
elk coördinatenstelsel hebben gevonden.
Het concept van een perfecte vloeistof is algemeen genoeg om een grote
verscheidenheid van vormen van materie te beschrijven. We specificeren
de toestandsvergelijking om de evolutie van een dergelijke vloeistof te
bepalen. De toestandsvergelijking relateert de druk aan de energiedichtheid,
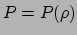 . Stof is een speciaal geval waarvoor
. Stof is een speciaal geval waarvoor 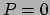 , terwijl een
isotroop gas bestaande uit fotonen
, terwijl een
isotroop gas bestaande uit fotonen
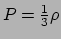 heeft.
Een meer exotisch voorbeeld is de energie van het vacuum, waarvoor de
energie-impuls tensor evenredig is met de metriek,
heeft.
Een meer exotisch voorbeeld is de energie van het vacuum, waarvoor de
energie-impuls tensor evenredig is met de metriek,
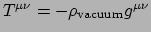 . Het idee van een energiedichtheid
van het vacuum is zinloos in de SRT, omdat daar de absolute schaal
van de energie niet relevant is, enkel energieverschillen tussen toestanden.
In de ART koppelt alle energie echter met gravitatie (en veroorzaakt kromming
van ruimtetijd), en wordt de mogelijkheid van het bestaan van vacuumenergie
een belangrijke beschouwing.
. Het idee van een energiedichtheid
van het vacuum is zinloos in de SRT, omdat daar de absolute schaal
van de energie niet relevant is, enkel energieverschillen tussen toestanden.
In de ART koppelt alle energie echter met gravitatie (en veroorzaakt kromming
van ruimtetijd), en wordt de mogelijkheid van het bestaan van vacuumenergie
een belangrijke beschouwing.
Behalve dat
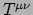 symmetrisch is, heeft hij de belangrijke eigenschap
dat hij behouden is. Energie- en impulsbehoud wordt uitgedrukt door het feit dat
de divergentie gelijk is aan nul,
symmetrisch is, heeft hij de belangrijke eigenschap
dat hij behouden is. Energie- en impulsbehoud wordt uitgedrukt door het feit dat
de divergentie gelijk is aan nul,
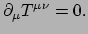 |
(225) |
Bovenstaande uitdrukking is een verzameling van vier vergelijkingen, een voor
elke waarde van 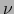 . De uitdrukking met
. De uitdrukking met 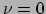 correspondeert met
energiebehoud, terwijl
correspondeert met
energiebehoud, terwijl
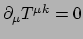 met
met 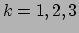 behoud
van de
behoud
van de 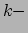 de component van de impuls uitdrukt. Laten we dit eens toepassen
op de perfecte vloeistof. We vinden dan
de component van de impuls uitdrukt. Laten we dit eens toepassen
op de perfecte vloeistof. We vinden dan
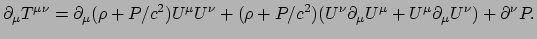 |
(226) |
Om te analyseren wat deze uitdrukking betekent, is het nuttig om afzonderlijk
te beschouwen wat er gebeurt als we een en ander projecteren langs en loodrecht
op het viersnelheidsveld 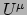 . Allereerst merken we
op dat de nomalisatie
. Allereerst merken we
op dat de nomalisatie
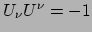 de volgende identiteit levert,
de volgende identiteit levert,
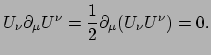 |
(227) |
Projecteren komt neer op contraheren met 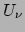 en we vinden
en we vinden
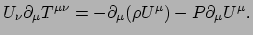 |
(228) |
Als we dit gelijkstellen aan nul vinden we de relativistische vergelijking
voor energiebehoud van een perfecte vloeistof. Het ziet een vertrouwder uit
in de niet-relativistische limiet, waar geldt
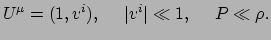 |
(229) |
De laatste vergelijking is aannemelijk, omdat druk enkel van de random
bewegingen van de individuele deeltjes komt, en in deze limiet zijn deze
bewegingen (net als de beweging van de bulk met 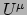 ) klein. We
vinden dus in niet-relativistische taal
) klein. We
vinden dus in niet-relativistische taal
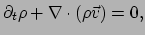 |
(230) |
hetgeen de continuïteitsvergelijking is voor de energiedichtheid.
Tenslotte gaan we naar het deel van vergelijking (232)
dat loodrecht staat op de viersnelheid. Om een vector loodrecht op 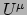 te projecteren, moeten we die vermenigvuldigen met de projectie tensor
te projecteren, moeten we die vermenigvuldigen met de projectie tensor
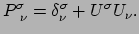 |
(231) |
We kunnen controleren dat bovenstaande projectie tensor zijn werk doet
door een vector
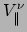 parallel aan
parallel aan 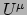 en een andere vector
en een andere vector
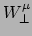 loodrecht op
loodrecht op 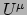 te nemen. We vinden dan
te nemen. We vinden dan
Toepassen op
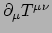 levert
levert
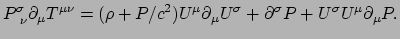 |
(233) |
We interpreteren deze vergelijking in
de niet-relativistische limiet. Als we de ruimtelijke componenten
gelijkstellen aan nul, vinden we
![$\displaystyle \rho \left[ \partial_t \vec v + ( \vec v \cdot \nabla ) \vec v \right]
+ \nabla P + \vec v( \partial_t P + \vec v \cdot \nabla P ) = 0.$](img1165.png) |
(234) |
Merk op dat de laatste paar termen afgeleiden hebben van 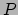 keer
de driesnelheid
keer
de driesnelheid 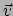 , waarvan we aannemen dat die klein is. Deze
termen zijn verwaarloosbaar ten opzichte van de
, waarvan we aannemen dat die klein is. Deze
termen zijn verwaarloosbaar ten opzichte van de 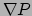 term. We
houden dan over
term. We
houden dan over
![$\displaystyle \rho \left[ \partial_t \vec v + ( \vec v \cdot \nabla ) \vec v \right] = -\nabla P,$](img1167.png) |
(235) |
en dit is de vergelijking van Euler uit de vloeistofmechanica.




Next: Wiskunde II - Curvelineaire
Up: De speciale relativiteitstheorie
Previous: De extra traagheid van
Contents
Jo van den Brand
2009-01-31
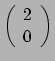 tensor
vertelt ons alles wat we moeten weten van de energie-achtige eigenschappen
van een systeem: energiedichtheid, druk, spanning, etc. Een algemene definitie
van
tensor
vertelt ons alles wat we moeten weten van de energie-achtige eigenschappen
van een systeem: energiedichtheid, druk, spanning, etc. Een algemene definitie
van